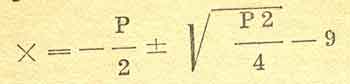
| Índice de El arte de aprender | Tercera parte Capítulo 2 El aprendizaje de los hechos. |
Tercera parte Capítulo 4 Se apende a sentir. | Biblioteca Virtual Antorcha |
|---|
TERCERA PARTE
¿Qué se debe aprender?
Capítulo 3
Nobleza de las ciencias abstractas. Fascinación que ejercen sobre el vulgo, al mismo tiempo que le inspiran terror. Combatir, ante todo, ese temor a lo abstracto en el alumno. Mostrarle que nada es más fácil de comprender que el razonamiento matemático. Necesidad moderna de saber matemática. Sus relaciones con la filosofía. Su elegancia.
Las ciencias que se llaman abstractas ejercen sobre el vulgo ignorante una especie de atracción religiosa, refrenada por el temor.
El vulgo adivina confusamente la nobleza de las especulaciones del espíritu que se ejercen sobre sí mismo, fuera de toda materialidad; presiente la divina poesía de los números. Pero la altura misma de tales pensamientos le da vértigo; le parece que, al dejar el sólido apoyo de la materia, su razón perderá el equilibrio; para designar una cosa incomprensible, el vulgo dice a menudo: Eso es álgebra..., opinión confirmada por gentes que se dicen cultas y por personas que tienen estudios que, no siendo nada tontos y no creyendo serlo, declaran con serenidad que no comprenden nada de matemáticas. Aun en los medios favorables al estudio, en las escuelas, alumnos que son aplicados en las otras materias, y hasta brillantes en literatura e historia, aceptan sonriendo los últimos lugares en los concursos de las ciencias abstractas.
¿Existe, realmente, una diferencia radical entre la capacidad para las ciencias abstractas y la adaptación a las ciencias reputadas como no-abstractas? Por ejemplo, un buen espíritu medio que comprende la gramática latina y que no puede imaginarse que alguien no la entienda, ¿podrá ser tan cerrado a la comprensión del álgebra?
Yo respondo, quizás audazmente: ¡No!
Y para tranquilizar al neófito, agrego, sin la menor paradoja, que las ciencias abstractas son, entre todos los ejercicios del espíritu, el más fácil. Si no te parece así, es por una extraña prevención, por una especie de neurastenia intelectual.
Si tuviera a mi cargo educar a un niño, me aplicaría en prevenirlo contra ese miedo a las abstracciones, desde que su inteligencia empezara a adquirir lucidez, como una madre previsora se esfuerza por sacarle el temor a las tinieblas o a la soledad.
No le diría jamás:
Vamos a tratar de comprender una abstracción. Le enseñaría todas las nociones abstractas que ha asimilado, sin dudar, pensando absorber algo concreto, algo material. ¡Cuántas abstracciones se encuentran en las palabras de la lengua que habla! Las palabras esperanza, esperar, semejante, ¿no son abstracciones, después de las cuales las x y las y de una ecuación son realidades casi groseras? En el campo de las abstracciones numéricas, desde que se ha dicho: dos y dos son cuatro, es decir, desde que se ha proclamado el principio de que un número se funde con otro para formar un tercero dotado de propiedades nuevas, se ha jugado locamente con lo abstracto.
Ahora bien, todo el mundo vive en una intimidad cordial con esas abstracciones, puesto que la realidad correspondiente nos es familiar. El espíritu se espanta ante la abstracción cuando se presenta aislada de las realidades que la sostienen originariamente. Toma a un hombre adulto que sea inteligente, pero que no haya estudiado nunca matemática, y escríbele en el encerado la siguiente igualdad:
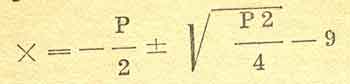
No pretendas hacerle comprender lo que eso significa; creo que está fuera del alcance del más maravilloso profesor. Sin embargo, el más perezoso de los bachilleres terminaría por comprenderlo en la clase del profesor más mediocre, precisamente porque esa ecuación está relacionada en la enseñanza con toda una cadena de abstracciones, que van a parar, ni más ni menos, a: dos y dos son cuatro.
Para evitar esa paralización del espíritu del neófito ante lo abstracto, lo mejor es partir de lo concreto, de lo material. A los niños debe enseñárseles la aritmética con objetos. En cuanto a la geometría, si abro un libro y en la primera página veo: La geometría es la ciencia... que..., etc., lo echo inmediatamente al cesto de los papeles.
¿Cómo comenzar, entonces, una geometría elemental?
A fe mía, que no lo he pensado nunca; pero creo que la empezaría, más o menos, así:
Alrededor de cinco mil años antes de Jesucristo, hubo en Egipto un pueblo de agricultores muy inteligentes; como todos los agricultores, los egipcios sembraban más o menos trigo en parcelas más o menos grandes de tierra; compraban o vendían un campo más o menos caro, según fuera más o menos vasto. Sintieron, entonces, la necesidad de saber exactamente cuántas veces una parcela de tierra era mayor que tal otra; esto era, evidentemente, más difícil que evaluar dos sacos diferentes de trigo, puesto que el campo no es manejable y puede tener cualquier forma; concibieron, entonces, la idea de trazar líneas regulares en los campos irregulares, por ejemplo, tres líneas que se cortan, lo que se llama triángulo, que es evidentemente más fácil de comparar con otro triángulo, que dos tierras de forma extravagante.
He aquí cómo empezaría yo un tratado de geometría elemental; además, esto sería menos aburrido que: La geometría es la ciencia que... Sigo creyendo que mi método sería más fácil de comprender.
Bien, querido lector, todas las ciencias matemáticas parten de realidades tan visibles y tan tangibles como la geometría. Además, debes retener esto: no hay más que UNA ciencia matemática, la geometría, madre del álgebra, de la mecánica, de la astronomía, de todo. Todo el gasto de x y de y proviene del humilde triángulo que los boyeros egipcios trazaban sobre su negro y fértil suelo cinco mil años antes del siglo de Augusto. Reconfórtate, pues, con la idea de que tantas abstracciones que parecen al profano jugar en el empíreo -como las esferas armoniosas del Sueño de Escipión (1) -, están tan enraizadas en la tierra como el trigo.
Pero si esto no es bastante para conjurar el terror de ciertos espíritus frente a las ciencias exactas, no hay nada mejor que asentar la enseñanza sobre lo real; así no podrán escapar a la necesidad del razonamiento y de la deducción abstracta; deberá decirse: supongamos que..., dado que..., ahora bien..., entonces... Aun cuando no se irrite frente a la abstracción, el espíritu se entorpece frente al razonamiento; se entorpece o se dispersa. Además, aprender es un acto de voluntad, en esto más que en ninguna otra cosa, puesto que, machacando obstinadamente, se puede enseñar hasta a un haragán, casi a pesar suyo, la historia de la Revolución francesa; ¿pero cómo enseñar a ese mismo estudiante rebelde el teorema de las tres perpendiculares, si rehusa seguir el razonamiento? Aquí puedes palpar el verdadero motivo por el cual tantas personas dicen sinceramente:
Yo no comprendo las matemáticas.
Lo que significa:
Yo no dispongo de la voluntad necesaria para fijar mi atención sobre un razonamiento.
Si existen verdaderamente espíritus que no comprenden la matemática, cualquiera que sea la atención que pongan, pueden muy bien extenderse a sí mismos un certificado de estupidez, puesto que la matemática -pongamos, por ejemplo, el teorema de las tres perpendiculares- es una serie de proposiciones gramaticales, cada una de las cuales contiene sujeto, verbo y atributo, en una palabra, construídas sobre el modelo de las proposiciones más usuales. La frase: Tiremos una línea del punto A al punto B, me parece tan clara como decir: tomemos por la Avenida Kléber para ir del Trocadero a la Estrella. La frase: transportemos el triángulo A B C sobre el triángulo A' B' C', no exige para entenderla más que la inteligencia del que entiende: cerremos esta caja con su tapa. Cada frase del teorema es perfectamente clara; si no la comprendes es porque estás enfermo.
¿Qué es lo que podría impedirte, no siendo enfermo, la comprensión de todo el teorema?
O bien que estés distraído durante una de esas frases tan claras, o bien que el maestro haya omitido una que sea útil, o que, demasiado embebido en la verdad que demuestra, haya saltado demasiado rápidamente sobre las intermediarias; es éste un caso frecuente en los profesores de geometría y en los autores de libros de matemática: no se dan cuenta de la cantidad de explicaciones requeridas por la inteligengcia del alumno. Un teorema que se demuestra, es un camino que se traza entre una verdad y otra; los buenos profesores y los buenos libros hacen ese camino lo más llano posible y, sobre todo, continuo; los malos libros y profesores dejan sobre él asperezas y, sobre todo, olvidan trazar los caminos ya recorridos. ¿Cómo extrañarnos, pues, de que el alumno se desanime o se pierda?
Así, la pretendida dificultad especial para la geometría y todas las ciencias exactas que derivan de ella, consiste solamente en esto:
Que la atención no debe desfallecer, ni por un instante, durante la demonstración.
Que la demonstración debe ser rigurosamente continua; que, entre frase y frase, no haya ninguna falla, de manera que, de una frase a la otra, la progresión tenga un carácter de evidencia.
De estas dos dificultades, una concierne al estudiante; la otra al maestro o al libro; la que concierne al aprendiz es pequeña, puesto que, por lo menos en la matemática elemental, las proposiciones, aun suponiéndolas demostradas con la minuciosa progresión que yo recomiendo, no exigen un gran aparato demostrativo: son suficientes algunos minutos de atención continua. Cuando se llega a la matemática superior, el espíritu está hecho a ese género de atención, por lo que, lejos de ser un esfuerzo más rudo, creo que para un espíritu medianamente constituído la matemática es el más fácil de todos; no exige ningún don especial, salvo no padecer enfermedad del intelecto, pues como el sistema consiste en pasar de una evidencia a otra, la misma rigidez del procedimiento sostiene admirablemente el espíritu. Por lo demás, los hechos confirman esta previsión teórica: no existe ninguna materia más universalmente asimilada, en nuestros días, que la matemática. Ingenieros, contramaestres, obreros superiores de usinas eléctricas y químicas, oficiales y suboficiales de la marina y la artillería de todos los países, decidme: ¿hay alguna ocupación del espíritu que reúna más adeptos, reclutados en todas las clases sociales, que la matemática?
Entonces, si un discípulo de inteligencia media no comprende la matemática, puedes estar seguro que se le enseña mal: es malo el maestro o el libro; por lo demás, ambos pueden ser, al mismo tiempo, sabios y malos. En ese caso, el maestro o el libro no saben comunicar su ciencia. Tranquilizaremos al lector inmediatamente diciéndole que hay un gran número de buenos libros y profesores, sobre todo para enseñar los elementos de la matemática, lo que es otra prueba de su facilidad. Es casi imposible, cuando se escribe un libro de álgebra o de trigonometría para principiantes, ser desordenado, oscuro o prolijo, como, por ejemplo, cuando se escribe una historia, una geografía o una gramática. Sería necesario ser un maestro ininteligible para no enseñar claramente el famoso teorema acerca del cuadrado de la hipotenusa o las ecuaciones de segundo grado.
Está demostrado, pues, que es fácil aprender las ciencias exactas; pero, ¿es útil?
Creo que es indispensable.
Un hombre que no sabe cómo se evalúa a distancia la altura de un campanario, cómo se demuestra el principio de Arquímedes, que ignora la teoría de las fracciones, que no ha oído hablar nunca de la propagación de las ondas, se pasea por la vida contemporánea como un ciego o, si se quiere, como un niño. Ahora bien, si yo no entiendo de música, lo que tengo que hacer es no asistir a donde se haga un culto de ella; pero, ¿qué medio puede usarse para ir, en el siglo veinte, a donde no reine la ciencia? Está en todas partes, nos rodea y nos gobierna. Se nos aparece, es verdad, en sus aplicaciones; pero no te dejes engañar: la matemática está inmediatamente detrás de los milagros que ven tus ojos. Sin ella es imposible comprender la física, la química y la biología moderna de nuestro tiempo, a pesar de que parecen al profano ciencias en frascos, balanzas, hornos o bisturíes, en lugar de x y de y. Sin ella es imposible comprender la filosofía moderna, que se sirve del concurso y del testimonio de todas las otras ciencias. Así como la tierra soporta nuestras construcciones materiales, la geometría soporta todas nuestras especulaciones intelectuales.
Además de la ventaja de dar al alumno la verdadera clave del universo, las ciencias matemáticas son el mejor ejercicio de razonamiento que se le puede imponer. He nombrado ya la filosofía; sabes que los razonamientos filosóficos son infinitamente más sutiles, más complicados, en una palabra, más difíciles que los razonamientos matemáticos; no existe mejor entrenamiento que éstos para llegar a comprender aquéllos, para medir su valor y juzgarlos. Un espíritu acostumbrado a la geometría entra en la filosofía como en su propia casa; no se dejará sorprender por las semidemostraciones; verá inmediatamente los errores que ojos menos aguzados no ven; los evita hasta en sí mismo. Toda la teoría de Nietzsche sobre el Eterno retorno se basa en un grosero error matemático.
Quiero agregar, además, para inspirar a mi lector el deseo de aprender las ciencias exactas, que poseen una belleza intelectual incomparable; son, entre otras, las más elegantes. ¿Te sorprende la palabra? Debes saber que se emplea corrientemente, para designar un método ingenioso, la claridad instantánea de una demostración. Terminaré justamente este capítulo con el ejemplo de una demostración elegante, sacada de la aritmética elemental:
Tú sabes que se llaman números primos aquellos que no pueden ser divididos más que por sí mismos o por la unidad: 23 es un número primo, como lo es el 7 y el 3.
He aquí un teorema relativo a los números primos:
Todo número que no es primo admite, por lo menos, un divisor primo.
Demostración:
En efecto, todo número que no es primo admite un cierto número de divisores (Ésta es la definición). El menor de esos divisores es primo; de otro modo: si él admitiera divisores no sería el menor.
'¿No es encantador? ¿Está mal aplicado el epíteto de elegante a este hermoso juego del espíritu?
**NOTA**
(1).- Está refiriéndose al sueño de Escipión imaginado por Marco Tulio Cicerón en el libro VI de La República .NdE.
| Índice de El arte de aprender | Tercera parte Capítulo 2 El aprendizaje de los hechos. |
Tercera parte Capítulo 4 Se apende a sentir. | Biblioteca Virtual Antorcha |
|---|